题目链接
https://atcoder.jp/contests/abc335/tasks/abc335_g
题目大意
给定 \(n\) 个正整数 \(a_1,a_2,\cdots,a_n\) 和一个素数 \(P\)。求满足以下条件的二元组 \((i,j)\) 的个数。
\(1\leq i,j\leq N\) 。
存在正整数 \(k\) ,使得 \(A_i^k\equiv A_j\pmod P\)。
数据范围
- \(1\le n\le 2\times 10^{5}\)
- \(1\le a_i < P\)
- \(2 < P \le 10^{13}\) 且 \(P\) 是素数
解题思路
考虑同余式 \(x^k \equiv y \pmod P\) 能推出什么结论。
令 \(\delta_{P}(x)\) 表示 \(x\) 在模 \(P\) 意义下的阶,因为 \(x^k\) 和 \(y\) 在模 \(P\) 意义下同余,所以一定有 \(\delta_{P}(x^{k}) = \delta_P(y)\) 。
其实以上的转化是我看题解看到的,至于应该怎么想才能自然地想到这一步,感觉需要一定的数学直觉,并且需要靠多做题积累经验。
根据阶的性质,有 \(\delta_{P}(x^{k}) = \displaystyle\frac{\delta_{P}(x)}{\gcd(k, \delta_{P}(x))}\) ,所以可以得到 \(\delta_{P}(x) = \gcd(k, \delta_{P}(x)) \cdot \delta_{P}(y)\) ,所以我们能推出一个必要条件
$$ \[\begin{aligned} \exists{k \in \mathbb{N}} , x^{k} \equiv y \pmod P \implies \delta_{P}(y) \mid \delta_{P}(x) \end{aligned}\]$$
那么该条件的充分性是否成立呢。
lemma 1
如果 \(ta \equiv tb \pmod {tc}\) ,则 \(a \equiv b \pmod c\) 成立,其中 \(t,a,b\in \mathbb{N_{+}}\) 。
证明非常简单,只需要把取模运算的表达式写出来即可证明。
假设 \(g\) 为 \(P\) 的一个原根,根据原根的性质,一定存在 \(e_1\) 和 \(e_2\) 使得 \(g^{e_1} \equiv x \pmod P\) ,\(g^{e_2} \equiv y \pmod P\),两边取离散对数有 \(e_{1} \equiv \operatorname{ind}_{g}(x) \pmod{P-1}\) ,\(e_{2} \equiv \operatorname{ind}_{g}(y) \pmod{P - 1}\) 。我们要证 \(\exists{k \in \mathbb{N}} , x^{k} \equiv y \pmod P\) ,即证 \(\exists{k \in \mathbb{N}} , ke_{1} \equiv e_2 \pmod{P-1}\) 。
根据条件有
$$ \[\begin{aligned} \delta_{P}(y) \mid \delta_{P}(x) \iff\delta_{P}(g^{e_2}) \mid \delta_{P}(g^{e_1}) \iff \displaystyle\frac{P-1}{\gcd(e_2, P-1)} \mid \displaystyle\frac{P-1}{\gcd(e_1, P-1)} \iff \gcd(e_1, P-1) \mid \gcd(e_2, P-1) \end{aligned}\]$$
令 \(t = \gcd(e_1, P - 1)\) ,根据 lemma 1 和要证的式子 \(ke_{1}\equiv e_2 \pmod{P-1}\) ,有
$$ \[\begin{aligned} k\frac{e_1}{t} \equiv \frac{e_{2}}{t} \pmod{\frac{P-1}{t}} \end{aligned}\]$$
因为 \(\displaystyle\frac{e_{1}}{t}\) 与 \(\displaystyle\frac{P-1}{t}\) 互质,所以有
$$ \[\begin{aligned} k\equiv \frac{e_{2}}{t} \cdot \left(\frac{e_1}{t}\right)^{-1} \pmod{\frac{P-1}{t}} \end{aligned}\]$$
所以条件的充分性成立,即
$$ \[\begin{aligned} \exists{k \in \mathbb{N}} , \text{ }x^{k} \equiv y \pmod P \implies \delta_{P}(y) \mid \delta_{P}(x) \end{aligned}\]$$
接下来,考虑如何求一个数 \(a\) 在模 \(P\) 意义下的阶 \(\delta_{P}(a)\) 。因为 \(\delta_{P}(a) \mid (P - 1)\) ,并且若 \(\delta_{P}(a) \mid b\) ,那么 \(x^{b} \equiv 1 \pmod P\) 成立,所以可以先将 \(P - 1\) 质因数分解,初始时令 \(b = P - 1\) ,每次选取一个质因数 \(p\) ,判断 \(x ^ {\frac{b}{p}} \equiv 1 \pmod P\) 是否成立,成立则将 \(p\) 除掉,不成立就取下一个质因数做相同的操作,这样最后得到的 \(b\) 就是 \(a\) 的阶。对于给定序列的每一个 \(a_i\) 做一遍上述操作的时间复杂度为 \(O(\sqrt{P} + n \log^{2} P)\) 。
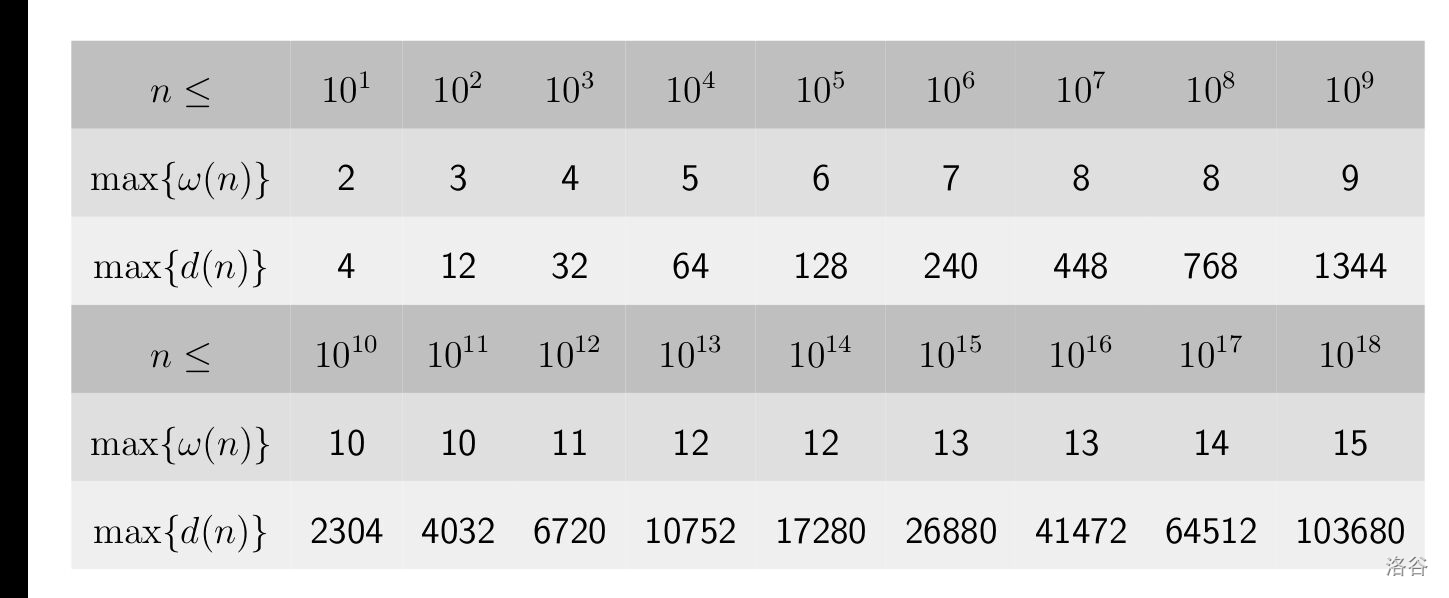
根据上表,我们发现 \(P - 1\) 的约数个数的级别不超过 \(10^4\) ,所以可以直接 \(O(\operatorname{d}(P)^{2})\) 计算 \(\delta_{P}(a_i)\) 对答案的贡献。
所以总时间复杂度为 \(O(\sqrt{P} + n \log^{2} P + \operatorname{d}(P)^{2})\) ,时限为 \(5\text{s}\) ,可以通过本题。