TLE_Automatの小窝

待施工ing

I. 起因

之前打比赛多次担心写单哈希被卡，但 N 神之前说他高中打过的所有比赛，但凡是字符串的题写 unsigned long long 自然溢出从来没被卡过。我信以为真，认为现在已经没有人素质差到卡别人单模哈希。后来我打了一些 AtCoder 的比赛也写了很多 ull 自然溢出也没事。直到 这场CF N 神 B 题 ull 自然溢出被卡到裂开，以为思路错了，直到赛后才发现是单哈希被卡了。

Brief

NEUQ 寒假集训自主刷题记录，比较 trivival 会简记一下思路，比较困难会写解题报告或者题解记录一下。

解题思路

先考虑几个必要条件：

• \(x\) 结点是 ( 且 \(y\) 结点是 )。
• \(x\) 到 \(y\) 至少有一条路径经过偶数个结点。

在此之外，我们注意到如果路径的开头存在连续两个 (，那么可以在上面来回走来刷左括号；如果路径的结尾存在两个 )，那么可以在上面来回走来刷右括号。

那么一个初步的想法就是：

• 如果 \(x\) 可以直接沿着左右括号交替的路径走到 \(y\)，那就做完了。
• 否则，从 \(x\) 沿着交替的左右括号一直走，走到某一个 ((，然后开始刷足够多的左括号，然后原路返回 \(x\)，再从 \(x\) 沿着某条经过偶数个结点的路径走到 \(y\)，从 \(y\) 沿着交替的左右括号一直走，走到某一个 ))，然后开始刷右括号，刷到与剩下的左括号平衡，然后返回 \(y\)​ 即可。

题目链接

https://atcoder.jp/contests/abc352/tasks/abc352_g

题目大意

总共有 \(N\) 种不同颜色的袜子，第 \(i\) 种颜色的袜子有 \(A_i\) 只。现在高桥要按照以下规则决定早上穿哪一双袜子：

• 从当前剩余的袜子中等概率随机且不放回地抽取一只袜子。

• 若抽出的袜子颜色与之前某次抽出的袜子颜色相同，则停止操作并穿这种颜色的袜子；

  若抽出的袜子颜色与之前每一次抽出的颜色均不同，则进行下一次抽取操作。

求高桥抽取袜子次数的期望值，对 \(998244353\) 取模。

数据范围

• \(1 \le N \le 3\times 10^{5}\)
• \(2 \le A_i \le 3000\)

题目链接

https://atcoder.jp/contests/agc066/tasks/agc066_a

题目大意

给定一个 \(N \times N\) 的方阵 \(A_{i, j}\) 和一个正整数 \(d\)。每次可以花费 \(x\) 的代价将矩阵的某一个位置加上 \(x\) 或减去 \(x\)。请构造一种方案使得方阵中所有相邻位置的差的绝对值大于等于 \(d\)，且代价之和小于等于 \(\frac{1}{2}N^{2}d\)。

数据范围

• \(2\le N \le 500\)
• \(1\le d \le 1000\)
• \(-1000 \le A_{i, j} \le 1000\)

题目链接

https://codeforces.com/contest/1942/problem/E

题目大意

小 N 和小 J 各有 \(n\) 头奶牛，小 N 的奶牛位置为 \(a_1, a_2, \cdots, a_n\)，小 J 的奶牛位置为 \(b_1, b_2, \cdots, b_n\)。其中小 N 和小 J 的奶牛交替出现，且位置在 \(1\) 与 \(l\) 之间，即满足 \(0 < a_1 < b_1 < a_2 < b_2 < \cdots < a_n < b_n < l + 1\) 或 \(0 < b_1 < a_1 < b_2 < a_2 < \cdots < b_n < a_n < l + 1\)。

现在小 J 和小 N 轮流进行以下操作，小 J 先手：

• 当前操作的人任意选中自己的 \(k(1 \le k \le n)\) 头奶牛，并且让这些奶牛一起向左或向右移动一格。移动后，位置不能与另外一个人的奶牛重合，也不能超出边界（即位置不能小于 \(1\) 也不能大于 \(n\)）。
• 若无法进行上述操作，当前操作的人判负。

问有多少种合法的序列组合 \((a, b)\)，使得小 J 必胜（两人均足够聪明）。

数据范围

多组测试数据，保证

• \(2 \le l \le 10^6 , \sum l \le 10^{6}\)
• \(1 \le n \le \left\lfloor\frac{l}{2}\right\rfloor\)

题目链接

https://codeforces.com/contest/1929/problem/E

题目大意

给定一颗 \(n\) 个结点的树，给定 \(k\) 条树上的路径 \(a_i, b_i\)。现在要对树上的一些边染色，使得 \(k\) 条路径中的每一条路径上都至少有一条边被染色，问最少染多少条边。

数据范围

• \(2\le n \le 10^{5}\)
• \(1 \le k \le 20\)

题目链接

https://atcoder.jp/contests/arc171/tasks/arc171_c

题目大意

给定一颗 \(N\) 个节点的树，初始时编号为 \(i\) 的物品放在编号为 \(i\) 的节点上。

你可以进行以下操作任意多次（可以为 \(0\) 次）：

• 选择一条未被删除的边，假设这条边的两个端点编号分别为 \(u,v\)，交换节点 \(u, v\) 上的物品，并且将这条边删除。

设 \(a_i\) 为最终编号为 \(i\) 的节点上的物品编号，那么通过上述操作能形成多少种不同的序列 \((a_1, a_2, \dots, a_n)\)，答案对 \(998244353\) 取模。

数据范围

• \(1\le N \le 3\times 10^{3}\)

题目链接

https://codeforces.com/contest/1925/problem/F

题目大意

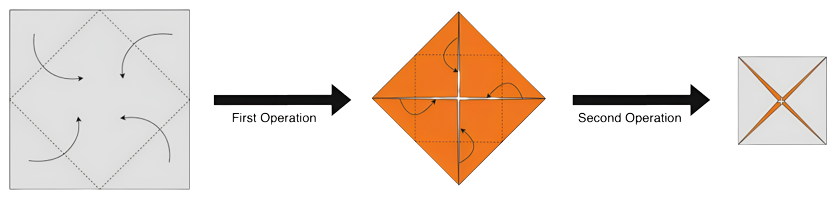
将一个边长为 \(1\) 的正方形按如图所示的方法进行 \(N\) 次折叠（上图为 \(N = 2\) 的情况），折叠之后展开。

展开后的折痕分为两种，一种是向内凹陷的折痕，总长度记为 \(V\)，另外一种是向外凸出的折痕，总长度记为 \(M\)。

可以证明 \(\displaystyle\frac{M}{V} = A + B\sqrt{2}\)，其中 \(A,B\) 均为有理数。求 \(B\) 对 \(999\text{ }999\text{ }893\) 取模的结果。

数据范围

• \(1\le N \le 10^{9}\)